Giải bài toán xác suất không còn là thử thách khó nhằn khi bạn nắm vững các bước phân tích và áp dụng đúng phương pháp. Bài viết này Hoidap247 sẽ hướng dẫn bạn cách tiếp cận, phân loại và giải giúp tăng hiệu quả học tập, tự tin vượt qua mọi bài tập.
Các công thức tính tổ hợp phổ biến nhất
Để hiểu rõ cách giải bài toán xác suất ngẫu nhiên một cách chính xác, bạn cần làm quen với phương pháp tính và công thức tổ hợp. Đây là công cụ toán học quan trọng dùng để đếm số cách lựa chọn các phần tử từ một tập hợp xác định như sau:
Tổ hợp có lặp
Trong các bài toán xác suất có mức độ phức tạp cao, việc tính toán số tổ hợp có lặp đóng vai trò rất quan trọng. Giả sử bạn có một tập hợp A gồm n phần tử và bạn muốn chọn ra k phần tử trong đó, với khả năng mỗi phần tử có thể được chọn nhiều lần mà không giới hạn.
Tổ hợp có lặp chập k từ tập hợp A là một tập con gồm k phần tử, trong đó mỗi phần tử có thể xuất hiện lặp lại nhiều lần. Công thức tính số tổ hợp dạng này giúp bạn giải quyết các bài toán mà phần tử được phép chọn nhiều lần. Công thức:
C(k,n) = C(k,n+k-1) + C(m-1,n+k-1)
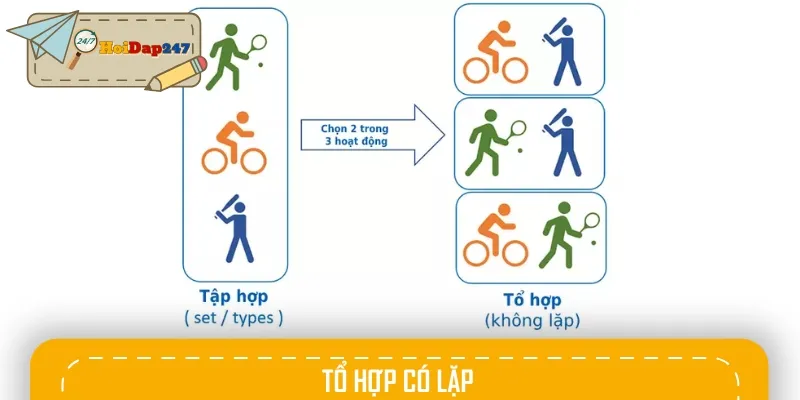
Tổ hợp không lặp
Khái niệm tổ hợp không lặp dùng để xác định số cách chọn các phần tử từ một tập hợp mà không cho phép chọn lại bất cứ phần tử nào đã lấy. Với tập hợp A gồm n phần tử, tổ hợp không lặp chập k là tập hợp gồm k phần tử khác nhau được chọn ra từ A, trong đó mỗi phần tử chỉ được chọn một lần duy nhất (1 ≤ k ≤ n). Công thức tính số tổ hợp không lặp được áp dụng như sau:
C(k,n) = A(k,n) / k! = n! / [k! × (n – k)!]
Hướng dẫn giải bài toán xác suất biến cố
Việc giải bài toán xác suất của một sự kiện giúp bạn đánh giá mức độ có thể xảy ra và hỗ trợ việc ra quyết định chính xác hơn. Xác suất được thể hiện dưới dạng giá trị nằm trong khoảng từ 0 đến 1, trong đó 0 đồng nghĩa với sự kiện không xảy ra và 1 thể hiện sự kiện chắc chắn xảy ra.
Để tính, đầu tiên cần xác định hai yếu tố quan trọng không gian mẫu toàn bộ các kết quả khả thi trong phép thử và sự kiện tập hợp các kết quả cụ thể mà bạn quan tâm. Khi đã rõ hai yếu tố này, bạn có thể sử dụng công thức tính xác suất cổ điển:
P(A) = n(A) / n(Ω)
Trong đó:
- P(A) chính là xác suất xảy ra của sự kiện A
- n(A) là số kết quả thuộc về sự kiện A
- n(Ω) là tổng số kết quả có thể xuất hiện trong không gian mẫu
Tổng hợp một số phương pháp giải bài toán xác suất thống kê
Để giải bài toán xác suất thống kê một cách hiệu quả, việc nắm vững các phương pháp cơ bản là vô cùng quan trọng. Những kỹ thuật này giúp bạn phân tích và xử lý dữ liệu một cách chính xác, đồng thời nâng cao khả năng tư duy logic trong các bài tập xác suất.
Tính xác suất tổng hợp
Công thức giải bài toán xác suất này được sử dụng khi muốn xác định khả năng xảy ra ít nhất một trong hai sự kiện A hoặc B. Theo đó, xác suất để một trong hai biến cố xảy ra là tổng của xác suất từng biến cố, trừ đi phần xác suất mà cả hai cùng xuất hiện nhằm tránh tính đếm trùng lặp. Phương pháp này rất hữu ích trong việc xử lý các trường hợp phức tạp và đảm bảo kết quả chính xác.
Biểu thức:
P(A hoặc B) = P(A) + P(B) – P(A và B)

Công thức xác suất biên
Xác suất biên là xác suất của một biến cố A xảy ra mà không phụ thuộc vào các biến cố khác. Khi phân loại các biến cố trong không gian mẫu thành từng nhóm riêng biệt, xác suất biên được tính bằng tổng các xác suất đồng thời của A với từng nhóm con đó.
Dạng tổng:
P(A)=i∑P(A∩Bi)
Nếu biến cố B là biến liên tục, công thức chuyển sang dạng tích phân:
P(A)=∫P(A∩B)dB
Công thức xác suất đồng thời xảy ra
Đây là công thức dùng để giải bài toán xác suất của việc hai biến cố A và B xảy ra cùng lúc. Xác suất đồng thời được tính bằng tích của xác suất biến cố đầu tiên với xác suất có điều kiện của biến cố thứ hai khi biết được biến cố đầu tiên đã xảy ra.
Công thức cụ thể:
P(AB) = P(A) x P(BlA)

Công thức tính có điều kiện
Xác suất có điều kiện biểu thị xác suất của một biến cố B xảy ra dựa trên giả thiết biến cố A đã xảy ra trước đó. Việc này giúp điều chỉnh xác suất ban đầu dựa trên thông tin đã biết, từ đó đưa ra đánh giá chính xác hơn. Cụ thể:
P(B∣A)=P(A)P(A∩B)
Mẹo giải bài toán xác suất hiệu quả cho học sinh
Để giải bài toán xác suất, học sinh cần áp dụng một số mẹo hữu ích. Những phương pháp này không chỉ giúp tiết kiệm thời gian mà còn nâng cao khả năng tư duy logic, từ đó cải thiện kết quả học tập trong môn xác suất và thống kê. Cụ thể:
- Hiểu rõ đề bài và xác định biến cố cần tính xác suất.
- Áp dụng chính xác các công thức xác suất cơ bản.
- Phân loại bài toán để chọn phương pháp giải phù hợp (cộng, nhân, điều kiện…).
- Vẽ sơ đồ, bảng để minh họa các trường hợp dễ hơn.
- Kiểm tra lại kết quả tránh sai sót do nhầm lẫn công thức.
- Học cách phân tích bài toán thành các bước nhỏ, dễ xử lý hơn.
Kết luận
Vừa rồi Hỏi đáp 247 đã chia sẻ những mẹo hữu ích giúp bạn giải bài toán xác suất hiệu quả hơn. Hy vọng các phương pháp này sẽ hỗ trợ bạn nắm vững kiến thức và tự tin vượt qua các bài tập một cách dễ dàng.

